About
Professor Gibin Powathil is an applied mathematician, focusing his research on interdisciplinary multi-scale approaches to utilise mathematics to understand the underlying complexity of various biological and biomedical problems in medicine and in particular, cancer.
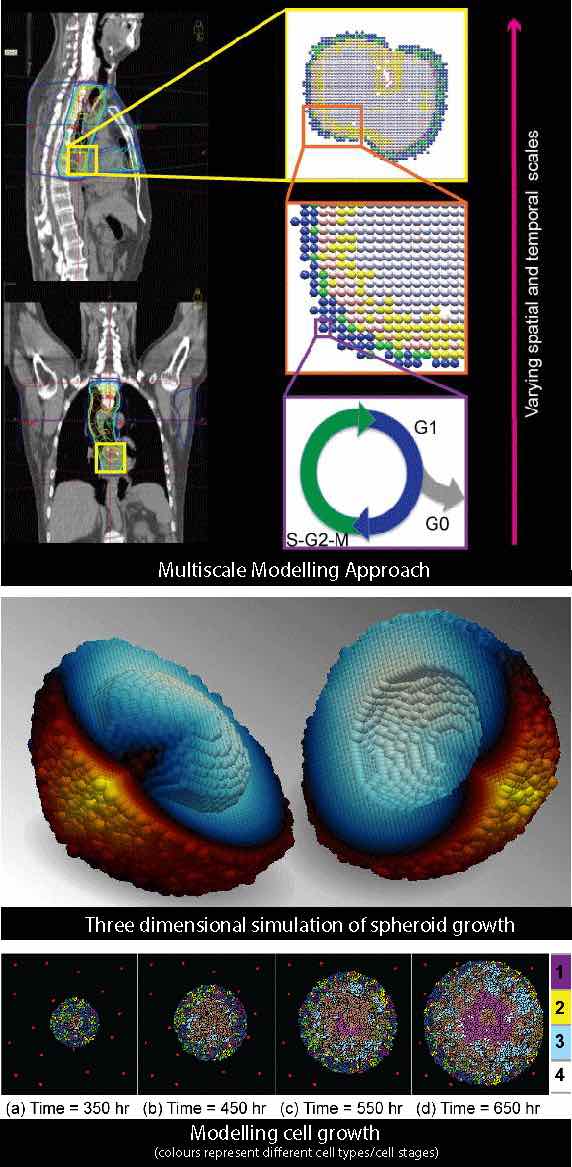
Currently, Gibin is working on developing multiscale models of cancer growth and treatment protocols to study various optimum treatment strategies; eventually to devise much needed predictive patient specific multimodality treatment regimes. These mathematical and computational models can be very helpful in gaining valuable insights into the mechanisms and consequences of various complex intracellular and intercellular changes during and after therapy.
Gibin received his PhD in Applied Mathematics from the University of Waterloo, Canada for his research on mathematical modelling of brain tumours. He has also received a MS in Computational Mathematics from National University of Singapore and MSc in Mathematics from Indian Institute of Technology, Madras, India.